Cryptography serves as the backbone for digital signature systems in cryptocurrencies, pivotal for confirming secure transactions between parties within a decentralized network. Today, a slew of cryptographic strategies are utilized by cryptocurrencies, aiming to bolster both efficiency and security in transaction frameworks.
Within the sphere of digital signature protocols, cryptocurrencies widely implement Elliptic Curve Cryptography (ECC). Notably, Bitcoin and Ethereum leverage the Elliptic Curve Digital Signature Algorithm (ECDSA) to authenticate their transactions.

Background of ECC and ECDSA
Elliptic Curve Cryptography was simultaneously proposed in 1985 by mathematicians Neal Koblitz and Victor S. Miller. Although it marked a significant advancement in cryptography, it wasn’t until the early 2000s, with the rise of the Internet, that ECC gained prominence, found favor among governments, and was integrated as an encryption tool by ISPs.
Compared to RSA encryption ECC holds a distinct advantage: the key sizes are drastically smaller compared to RSA encryption, yet they maintain equivalent security levels. Despite RSA being more prevalent on the Internet, ECC essentially functions as an optimized form of RSA, explaining its acceptance in cryptocurrencies.

Read: Delving into RSA Cryptography: A Comprehensive Overview of This Encryption Technique
The National Institute of Standards and Technology (NIST) in the U.S. endorses ECC among its 'recommended algorithms,' while the NSA employs 384-bit ECC keys for securing top secret information. As a showcase of ECC's efficiency versus RSA, a 384-bit ECC key serves the same purpose as a 7680-bit RSA key, illustrating its crucial role in reducing transaction sizes in blockchain networks. Suite B Elliptic Curve Cryptography operates using an algebraic curve structure over finite fields, forming a robust encryption method. It leverages a trapdoor function, relying on the practical impossibility of reverting a public base point to extract the discrete logarithm of an elliptic curve element.
How Does It Work
Within public-key cryptography, trapdoor functions make directionality simple from A → B, but reverse computation from B → A remains markedly difficult due to specific mathematical challenges. Similarly, RSA encryption is grounded in the principle where a multiplicand, serving as the private key, resists computation from defined starting variables. public-key The curve points must adhere to the equation depicted: (x, y) reside on this curve, characterized by constants a and b. Theoretical diversity offers limitless curves, yet specifically for Bitcoin and Ethereum, the dedicated curve, referred to as secp256k1, is deployed, as visualized below.
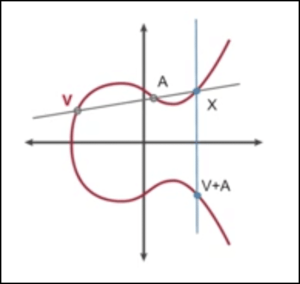
Elliptic curves exhibit symmetry about the x-axis. Drawing a line from any point on such a curve serves to intersect not more than three points on it. The intersection is traceable through two points, leading to a third; reflection of this intersection point across the x-axis reveals the summation of the first pair. Prime Factorization , and ECC relies on the concept of Point Multiplication In visualization, V and A pinpoint the initial points, X denotes the third point, while Z signifies the cumulative addition of V and A. In digital signature frameworks, the line’s origin is generally pre-decided.
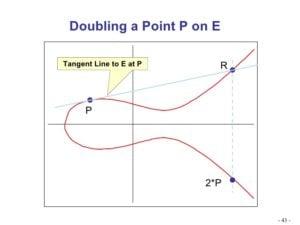
To craft a trapdoor function, ECC employs point multiplication, extending a predefined base point through iterative addition. For practical purposes, base point P serves as a base, where progression from 2P is calculated as demonstrated.
y^2 = ax^3+ b
Tracing a tangent from P to intersect R indicates reflection yielding 2P. The succession to compute subsequent points like 3P and 4P follows similarly, enabling illustration continuation.
This represents the graph's multiplicative property, essentially multiplying an integer across a fixed point yields resultant trapdoor function properties, integral to cryptographic strength.
Expressing a variable x through a 384-bit integer multiplied by base point P positions point Z on the curve, public within cryptocurrencies yet secreting x (the private key). Deriving x from Z and P necessitates determining the frequency of self-addition completing point Z.
In the realm of cryptocurrency digital signatures, four pivotal criteria dictate authenticity and ensure verification: 1) Signer authenticity verifiability, 2) Signature forgeries impossibility, 3) Signature non-repudiation assurance, 4) Private key derivation infeasibility from its public counterpart.
Elliptic Curve Cryptography adeptly adheres to these criteria, providing robust public key coordinates as (x, y), while a 384-bit integer forms the private key.
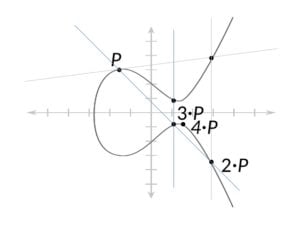
Assertions of knowledge regarding x can be made without direct disclosure, fostering credibility within digital signature frameworks tasked with long-term viability. discrete logarithm problem .
In the domain of digital signage for cryptocurrencies, ECC remains outstandingly secure, though emerging concerns address quantum computers and their potential power endangering ECC integrity. Albeit such eventualities are perceived as distant, modular arithmetic Hypothetical scenarios involving quantum computers demonstrate capability in solving specific mathematical dilemmas like ECC’s discrete logarithm, given sufficient power.
Use In Cryptocurrencies
Emerging cryptocurrencies are pre-emptively tackling quantum computing threats by integrating
- Certain algorithms into the backbone of digital signature schemes. Indeed, the NSA proclaimed its intention to eventually migrate from ECC to alternative ciphers in response to inevitable quantum computing prowess.
- Quantum Computation: Assessing the Risks to Bitcoin
- Speculative at present, the quantum computing capacity required for algorithms like Shor’s to resolve discrete logarithms vastly outpaces current quantum advances.
- Future-facing perspectives envision cryptocurrencies potentially evolving towards enhanced encryption for conducting secure transactions, with stalwarts like Bitcoin and Ethereum potentially adapting.
For the time being, ECC and its affinity for trapdoor function digital signatures safeguard as among the world's most secure encryption tactics, poised to hold their ground for the foreseeable future.
Blockchain enthusiast delving into content creation and web development, advocating for a decentralized Internet's promise and cryptocurrency advance. Reach out at brian@level-up-casino-app.com
Quantum Concerns
Spotlighting Six Crypto Initiatives Reinventing Web3 Learning Approaches Shor’s algorithm Contributing Opinion: Cryptocurrencies May Not Perfect the Future, Yet Decentralization Holds Societal Benefits
Contributing Opinion: The Dangers of Data Domination: Could Blockchain Foster Digital Despotism? quantum-resistant Regrettably, an efficient exploit of integer factorization equivalently undermines ECC reliability, since shared tactics solving initial challenges might impart adaptability against similarly complex, purportedly intractable problems.

All rights reserved. Registered Company No.05695741.
Conclusion
Blockfresh - Your Portal for Crypto, NFT & Metaverse Developments
Initiate a query by typing above and pressing Enter. To cancel, hit Esc.






1Telegram
Cryptography is the cornerstone of digital signature frameworks in cryptocurrencies, serving as the essential mechanism for verifying transactions securely between two entities in a decentralized ecosystem. Today's digital currencies employ a multitude of cryptographic strategies designed to ensure both efficiency and security in transaction handling.