What is RSA Cryptography? A Comprehensive Overview of This Encryption Technique

Cryptography Across the ages, the art of cryptography has served societies in diverse forms, morphing from the cryptic scripts of Egypt's ancient priests to the intricate algorithms we rely on over the Internet, making it an essential bridge for secure dialogue.

Widely recognized as the world's foremost asymmetric encryption algorithm, RSA cryptography became a reality through a series of remarkable advancements in cryptographic science and mathematics. Nowadays, virtually every Internet user leverages RSA cryptography in some capacity.

When delving into the realm of cryptocurrencies, you will find that many utilize a type of asymmetric encryption akin to RSA, known as Elliptic Curve Cryptography. Despite their differences, both operate on shared foundational principles, making a grasp of RSA beneficial for those looking to deepen their understanding of cryptographic systems within cryptocurrency networks.

Exploring Cryptographic Foundations: A Dive into Symmetric vs. Asymmetric Cryptography

Prior to the 1970s, cryptographic practices predominantly hinged on symmetric key systems. Here, mutual participants depended on a shared cryptographic key to both obfuscate the original text and decrypt the coded message. The shared key served as a confidential link yet came with inherent limitations and potential security flaws.

For example, both communicators need access to this secret key to encrypt and decrypt messages. Outside face-to-face interactions, significant effort is needed for its secure transmission via non-secure channels, which risks exposure to third parties potentially intercepting the key. Furthermore, symmetric encryption doesn't scale well; each unique communication line demands its distinct secret key—a cumbersome model impractical for cryptocurrency networks where many transactions take place.

The advent of asymmetric encryption provided an eloquent solution, frequently referred to as public key encryption. public-key cryptography Asymmetric encryption cleverly deploys a double-key system—one public, one private, transforming communication. You've got the public key available for all to send encrypted messages to its publisher, while the recipient employs the secret private key exclusively to decode these messages, obviating the need for secret key exchange.

This innovative encryption design took root from two pivotal concepts, first introduced in the groundbreaking work by the British mathematician James Ellis in 1970. Ellis envisioned encryption and its counterpart operation of decryption as inversely related yet distinctly separate via the application of dual keys.

James Ellis, image from The Telegraph .

Often illustrated with the analogy of a padlock and key, where the padlock symbolizes the public key and the key itself represents the private key, this model harnesses two central concepts for effective practical application.

• The Trapdoor Function
• The Diffie-Hellman Key Exchange

The Trapdoor Function

Among key cryptographic principles is the trapdoor function, crucial for allowing easy transition from one state to another while rendering reverse computation virtually impossible without special confidential information—the 'trapdoor.'

The trapdoor function underpinning the famed RSA cryptographic system is quintessentially Prime Factorization Prime factorization, an operation central to number theory, dissects composite numbers into their fundamental prime constituents. Recognizing that all non-prime numbers can be reduced to their prime components births significant implications for cryptographic strategies.

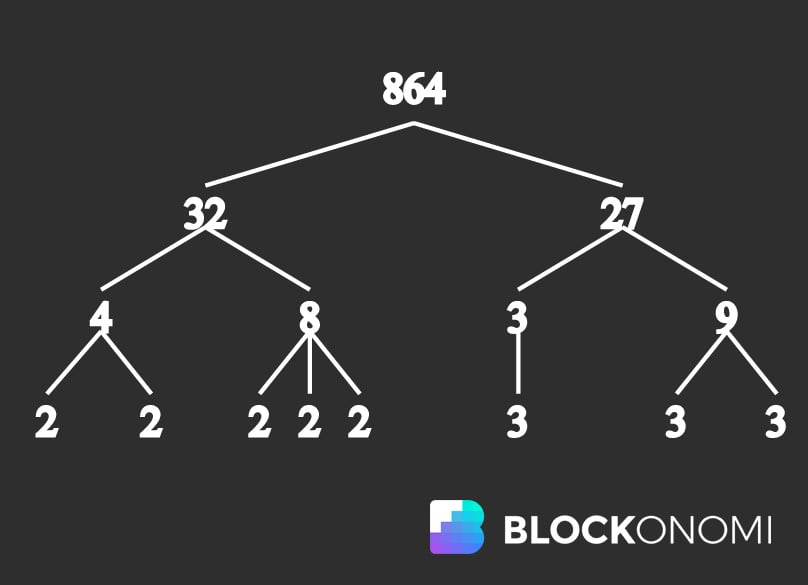
Understanding Prime Factorization, taken from Wikipedia

Given that breaking down excessively large prime numbers via prime factorization rapidly becomes impractical due to the vast trial and error required, there's currently no highly efficient algorithm capable of such factorization.

An extensive breakdown of RSA's engagement with prime factorization will follow, but first, it's vital to grasp the Diffie-Hellman Key Exchange.

The Diffie-Hellman Key Exchange

The Diffie-Hellman protocol stood as one of the earliest systems for safely exchanging cryptographic keys over open platforms without exposure. For broader comprehension, using abstract visualization of Diffie-Hellman Key Exchange and its affiliated sections, rather than pure mathematical jargon, simplifies understanding.

In illustrating the Diffie-Hellman process, many refer to it as the Secret Color Exchange.

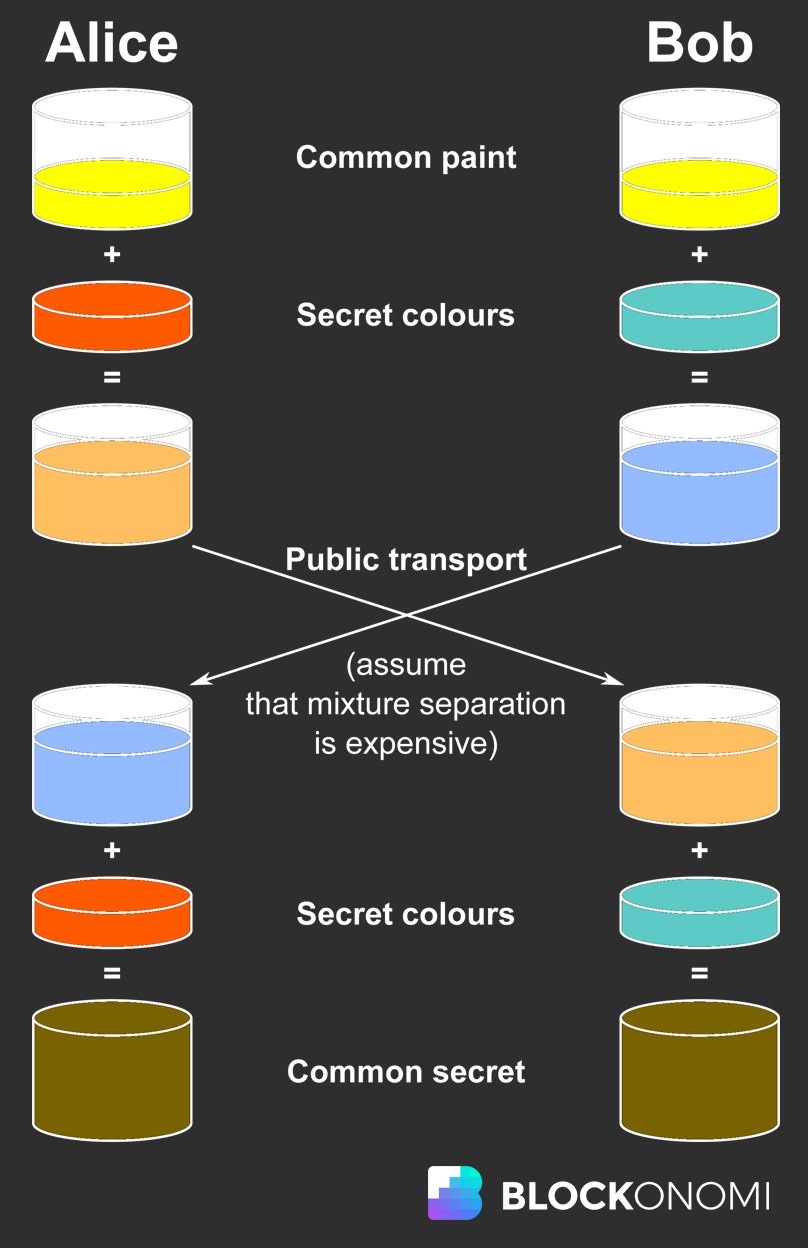
Visual representation of the Diffie-Helman Key Exchange borrowed from Wikipedia

The scenario rendering Alice and Bob's communications in an open arena exposes them to potential eavesdropping by Eve. The query remains: how can Alice and Bob cleverly utilize asymmetric encryption to maintain privacy without overtly communicating sensitive information?

Through establishing mutual secrets protected from overt exchange. The steps proceed as such:

Step 1

• Alice and Bob publicly choose Yellow as their standard color, well aware Eve overhears this.
• Yellow represents the public key.
• Alice's secret choice falls on Blue while mixing with the public Yellow, just as Bob discreetly adds Red to Yellow.
• These secret colors, Blue for Alice and Red for Bob, are their private cryptographic keys.

Step 2

• Alice and Bob combine their private colors with the public Yellow to create mixed hues.
• Alice's combination yields Green, and Bob's yields Orange.
• Alice and Bob proceed by sending each other their newly mixed colors.
• Eve, observing these color exchanges, faces a problem: these mixtures, acting as trapdoor functions, obstruct her reverse engineering attempts.
• Merging two colors to form a third is straightforward, but disentangling the original pair from the resulting color proves virtually impossible.

Step 3

• Alice and Bob incorporate their secret hues into the colors received, culminating in
  • Alice blending Blue into Bob's Orange.
  • Bob blending Red into Alice's Green.
  • Both mixtures result in Brown.

This example unravel how the Diffie-Hellman Key Exchange artfully enables secure communication. Though both Alice and Bob ultimately obtain the color Brown, they ingenously avoid sharing it, leaving Eve without vital clues necessary for deciphering their private message.

The above exemplifies Diffie-Hellman's elegance. Added with mathematical principles, assured protection of messages, central to RSA cryptography, utilizes prime factorization as its security mechanism.

How Does The RSA Algorithm Work?

In mechanics, the RSA procedure artfully combines both the enigmatic trapdoor of prime factorization and the Diffie-Hellman Key Exchange to ensure an asymmetric encryption standard, relying heartily on the formidable challenge of prime factorization.

1. Key Generation: Here, either a random number generator is utilized, or two vast primes, noted as p and q, are chosen. Keeping these confidential, they compute n=pq, defining the modulus applicable for both public and private realms, with its extensive magnitude representing key length. The public disclosure of 'n' follows. Current public key sizes, especially those surpassing 1024 bits, are immune to efficient algorithmic resolution of 'n.' Even supercomputing power would require extensive periods—up to millennia—to solve what's known as the RSA problem, a breakthrough capable of jeopardizing all RSA-coated cryptosystems.
2. Key Distribution: Consider Bob aims to convey confidential content to Alice. Below's the route taken.
   1. Access to Alice's public key is crucial for Bob to encode his communication.
   2. Alice exclusively retains her private key, necessary for decryption.
   3. Alice must reveal her public key to Bob to enable the sending of encrypted content.
   4. Alice, however, refrains from disclosing her private key.
3. Encryption follows, where after acquiring Alice's public key, Bob turns plaintext message (M) into integer form (m) via a set padding framework, encrypts via Alice's public key then dispatches ciphertext (c) to Alice.
4. Decryption: Alice utilizes her private key to extract message (m) from ciphertext (c) and reinstates original communication (M) by unearthing the padding framework from (m).

An expansive mathematical dissection dives deeper into RSA methodologies, accessible here , but is out of the scope of this article.

Digitally signing through RSA encryption, critical to cryptocurrencies, forms the bedrock of Bitcoin’s UTXO transactional architecture. Through signing, Alice verifies message authenticity to Bob (by showing private key usage) via hashing the message then appending it. Bob, deploying the same hash algorithm plus Alice’s public key, cross-verifies resultant with the true hash value, validating its source.

Conclusion

RSA encryption stands as the global cornerstone of asymmetric encryption techniques, trusted for its unmatched security that's yet to be unraveled by any algorithm. This method's robustness is credited to groundbreaking strides in cryptographic science and mathematical principles, notably the Diffie-Hellman Key Exchange and trapdoor functions. These innovations have propelled RSA into the foundational layer of secure global communications.